AI 井字棋

玩法

小时候九宫格中画 ⭕⭕❌❌ 的经典游戏。

但是

你根本不可能战胜它

算法

基于 （Minimax）极大极小博弈算法，具体算法度娘搜索一堆。

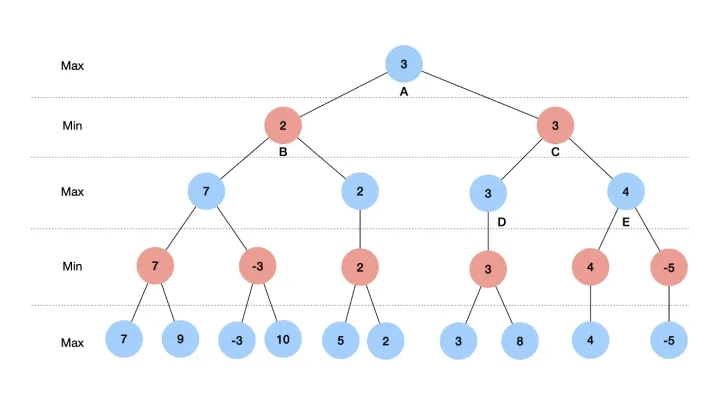
大小博弈 核心算法相对比较简单，真正难点在于 评估函数， 树结构最下方的 叶子结点 需要计算此结点的布局下的棋局评分， 对于棋手来说都希望选择评分对自己有利的棋局，如果评分以 ⭕ 为基准，那么轮到 ⭕ 方选择时，选择评分最高的布局结点， 如果 ❌ 方则选择评分最低（对⭕最不利也就是对❌最有利）的结点，因此也叫 极大极小博弈 算法。

由于只有 9 格，所以博弈深度直到 结束, 结束的评分必然只有三种结果：平局 ⭕胜利 ❌胜利， 所以分数 比较好定义，因此理论上这个 AI 是不可战胜的，实际上的确也是不可战胜的 😜。

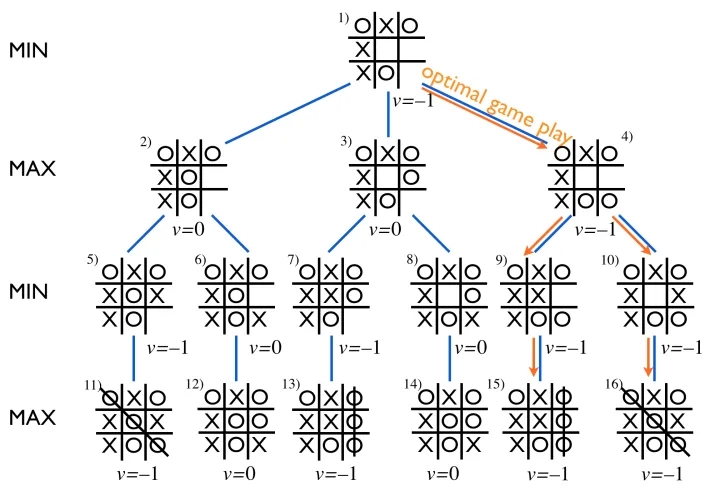
大小博弈算法封装函数

大小博弈算法计算量极其庞大，几乎就是遍历所有可能性，因此这里需要利用 α-β 剪枝 对没有必要再计算的分支进行剪枝（可查看 高亮 代码）。

import * as _ from "lodash";

export class MaxMinSearch {
  static MAX_SCORE = 2 ** 30;
  static MIN_SCORE = -(2 ** 30);
  root: any;
  maxDepth: number;
  getNextLevelState: Function;
  getEvaluateResult: Function;
  isLeafState: (any) => boolean;

  constructor(maxDepth = 5, root: any = null) {
    this.root = root;
    this.maxDepth = maxDepth;
  }

  getBestChoiceByState(
    state,
    isAi = true,
    depth = this.maxDepth,
    alpha = MaxMinSearch.MIN_SCORE,
    beta = MaxMinSearch.MAX_SCORE
  ): any {
    if (depth === 0 || (this.isLeafState ? this.isLeafState(state) : false)) {
      return this.getEvaluateResult(state, isAi);
    }
    let bestScore = isAi ? MaxMinSearch.MIN_SCORE : MaxMinSearch.MAX_SCORE;
    let bestChoice = null;
    const nextIt = this.getNextLevelState(isAi, state);
    for (const childState of nextIt) {
      const score = this.getBestChoiceByState(
        childState,
        !isAi,
        depth - 1,
        alpha,
        beta
      );
      if (isAi) {
        if (score > bestScore) {
          bestScore = score;
          if (depth === this.maxDepth) bestChoice = _.cloneDeep(childState);
          alpha = bestScore;
        }
      } else {
        if (score < bestScore) {
          bestScore = score;
          if (depth === this.maxDepth) bestChoice = _.cloneDeep(childState);
          beta = bestScore;
        }
      }
      if (nextIt.next) nextIt.next();
      if (alpha >= beta) break;
    }
    return depth === this.maxDepth ? bestChoice : bestScore;
  }

  setNextLevelState(func) {
    this.getNextLevelState = func;
    return this;
  }

  setEvaluateResult(func) {
    this.getEvaluateResult = func;
    return this;
  }

  setIsLeafState(func) {
    this.isLeafState = func;
    return this;
  }
}